哈夫曼树：它是由 n 个带权叶子结点构成的所有二叉树中带权路径长度最短的二叉树。因为这种树最早由哈夫曼（Huffman）研究，所以称为哈夫曼树，又叫最优二叉树。
路径：从树中一个结点到另一个结点之间的分支构成这两个结点间的路径

结点的路径长度：两结点间路径上的分支数。

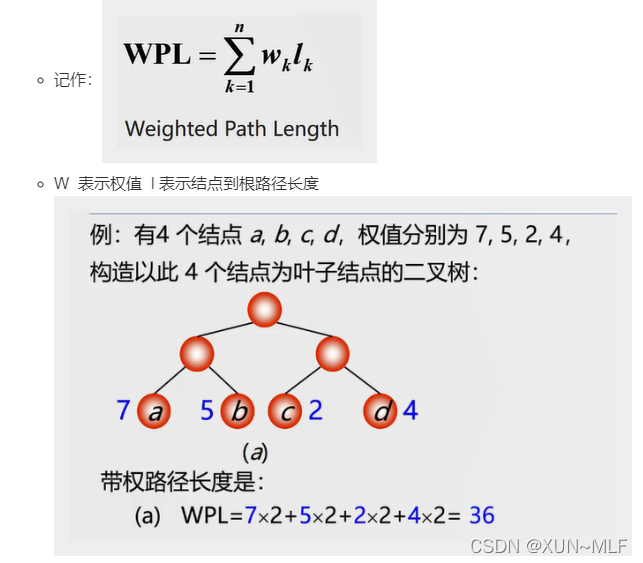
树的路径长度：从树根到每一个结点的路径长度之和。记作TL

结点树目相同的二叉树中，完全二叉树是路径长度最短的二叉树

权(weight):将树中结点赋给一个有着某种含义的数值，则这个数值称为该结点的权

结点的带权路径长度：从根结点到该结点之间的路径长度与该结点的权的乘积

树的带权路径长度：树中所有叶子节点的带权路径长度之和。

构造方法:

构造森林全是根

选用两小造新树

删除两小添新人

重复 2、3 剩单根



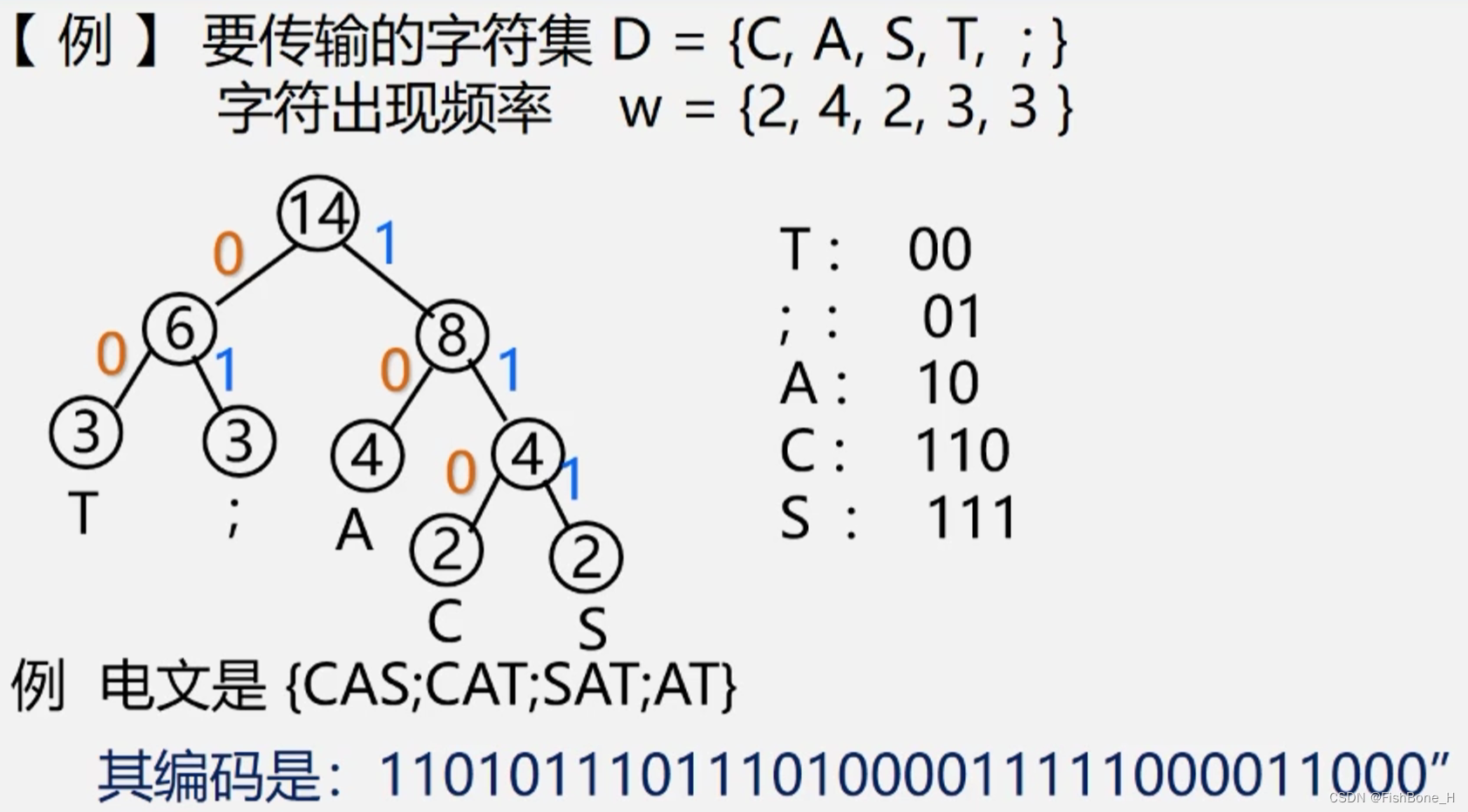
哈夫曼编码
统计字符集中每个字符在电文中出现的平均概率（概率越大，要求编码越短）

利用哈夫曼树的特点：权越大的叶子离根越近，将每个字符的概率值作为权重，构建哈夫曼树。则概率越大的结点，路径越短

在哈夫曼树的每个分支上标上0或1：

结点的左分支标0，右分支标1

把从根到每个叶子的路径上的标号连接起来，作为该叶子代表的字符的编码。